執行電池測試時,有許多參數可以透過量測物理量的時域分析 ( time domain analysis ) 獲得。有效的時域分析所著重除了量測精準度與解析度外,電池分析單元對量測頻寬與擷取時間掌握度也是相當重要。
以常見的參數:容量為例,特別是放電容量會將電池調整至滿荷電狀態 ( SOC:100% ) 後放電至截止條件 ( SOC:0% ) ,計量電池在過程中釋出的電量 ( charge amount ) 並標定為電池容量。電壓、電流、溫度等物理量可直接量測,電量則無法直接測得。庫侖法 ( Coulomb Counting ) 是一種常見電量計量方式,雖不如安培-小時一般直觀但庫侖是最早使用的電量單位,1安培電流定義為單位時間 (秒) 導體橫斷面通過1庫侖的電量,所以可以得知電量Q等同於電流I(t)對時間t的積分圖。
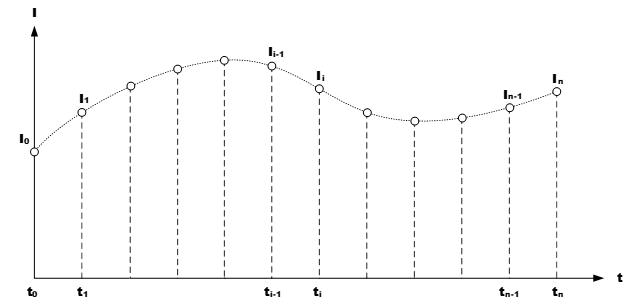
在某些情況下我們無法確切得知I(t),會透過定時量測/取樣的方式紀錄電流I如左圖獲得電流對時間分佈的離散數列。取得離散數列後可以透過梯形法 (Trapezoidal Rule) 取得近似積分值。
梯型法原理是透過區間梯型面積近似區間積分結果。
![]() Eq. 1
Eq. 1
t0至tn區間電流積分可表示如下,其中E為梯型法與實際積分之誤差值。
![]() Eq. 2
Eq. 2
假設I(t)在ti至ti+1是連續可微或稱作可解析的,令 ![]() 並對
並對![]() 作泰勒展開 (Tyler Expansion)
作泰勒展開 (Tyler Expansion)
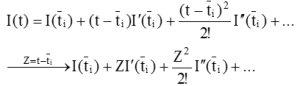 Eq. 3
Eq. 3
將泰勒展開式在ti至ti+1區間定積分
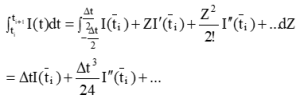 Eq. 4
Eq. 4
將泰勒展開式在ti至ti+1區間作梯型法
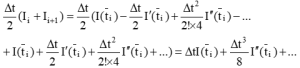 Eq. 5
Eq. 5
所以可以得知ti至ti+1區間,積分與梯型法誤差ei。
![]() Eq. 6
Eq. 6
t0至tN全域積分與近似法誤差E可表示為
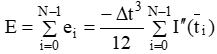 Eq. 7
Eq. 7
從上式 (Eq. 7) 可以得知梯型法近似積分的特性,其一:當電流為常數或時間一次函數時,電流對時間二階以上的導數即I’’(t) , I’’’(t) …為零,所以是沒有演算法產生的誤差。其二:透過縮減Δt可以大幅縮減演算法誤差,在實際應用令Δt即擷取資料時間1 Sec的演算法誤差為E1、0.1 Sec擷取時間演算法誤差為E2;依據下式 ( Eq. 8 ) 可以導出E1為E2之100倍。
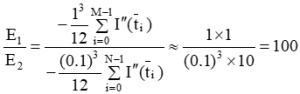 Eq. 8
Eq. 8



